Resumen de la semana
Introducción
En esta entrada les mostraremos un avance del resumen de la semana con sus debidas explicaciones para una mejor comprensión. El tema a tratar es: "las expresiones algebraicas". Esperamos que este resumen les ayude a comprender más el tema tratado en clase.
Expresiones Algebraicas
1. Polinomio: Es toda expresión algebraica racional entera (exponentes de la variables son enteros positivos o cero) formado por uno o más términos.
· Este polinomio está formado por cuatro términos que se identifican por estar separados por una suma o una resta.
2. Elementos:
· Variable: x
· Coeficientes: -9; 4; 5
· Exponentes: 0; 1; 2
§ El término cuadrático es:
§ El término lineal es:
§ El termino independiente: -8 (porque se sobrentiende que la variable está elevada a la cero)
Polinomios según su número de términos:
Monomio: Polinomio de un solo término.
Binomio: Polinomio de dos términos. Ej.
Trinomio: Polinomio de tres términos. Ej.
Polígono de 4 términos: Polinomio de cuatro términos. Ej.
§ (Los términos de un polinomio están separados por una suma o una resta)
Grado de un Monomio:
a Grado relativo (GR): El exponente respecto de
cada variable de la parte literal.
b Grado absoluto (GA): La suma de los exponentes
de las variables. (Se dice monomio de grado…)
Ejemplo:
Grado de un Polinomio:
a) GR: El mayor exponente de la variable en
referencia.
b) GA: El mayor grado absoluto de los términos
algebraicos que lo conforman.
Ejemplo:
Ejercicios:
Explicación: Te dan dos datos, te
dicen que el grado relativo de x es 7 y el grado absoluto es 12. Entonces es x
elevado a la 7, y para y tenemos que buscar un número que sumado con 2 te de 5
ya que 7 más 5 es 12 entonces este número sería el 3.
Explicación: te piden averiguar el valor
de m y te dicen que el grado absoluto es 10, entonces tienes que buscar un numero que sumado con 3
te de 10 y este número es 7 y el otro termino 7 más 1 sería 8 y el GA seguiría siendo el primer término. En conclusión m es 7.
Clasificación de Polinomios:
Ojo: ¡El polinomio homogéneo tiene un término de grado 6!
Polinomios especiales:
Polinomios opuestos: los coeficientes de los términos semejantes son opuestos.
Para que el polinomio Q sea
nulo:
Explicación: Para que el coeficiente sea nulo tendría
que ser menos 4 más 4 para que se eliminen y quede cero. Y en el segundo
término sería 0.
Para que el polinomio R sea homogéneo:
Explicación: Para que el polinomio sea homogéneo
todos los términos tienen que tener el mismo
grado absoluto, entonces si el GA del último término es 13, todos los demás
también tienen que ser 13. Entonces en el primer término buscas que numero
multiplicado por 5 más 3 te de 13 y ese número sería 2. Y en el segundo término
buscas que numero cuando le restes 6 y le sumes 2 y 8 te de 13, y ese número es
9.
Para que el polinomio S sea ordenado y completo respecto a x:
Explicación:
Para que un término sea ordenado y completo tiene que tener los exponentes en forma
creciente o decreciente y van desde el mayor exponente hasta 0. Entonces, en el último
término el exponente es cero. El tercer exponente sería 1. En el segundo término el exponente tendría que
ser dos y tienes que buscar un numero que multiplicado con 1 te de 2 y ese número
es 2. Y en el primer término tendría que ser 3 entonces tienes que buscar un
número que sumado con 1 te de 3 y ese número es 2.
Ejercicios:
1)
Dado el polinomio completo y ordenado en forma creciente,
Calcula m +n + p.
2)
Calcula el valor de m+n si el polinomio
P(x;y) es homogéneo
Video:
+18.50.30.png)
+18.50.30+-+Versio%CC%81n+4.png)
+18.50.30+-+Versio%CC%81n+3.png)
+18.50.30+-+Versio%CC%81n+6.png)
+18.50.30+-+Versio%CC%81n+5.png)







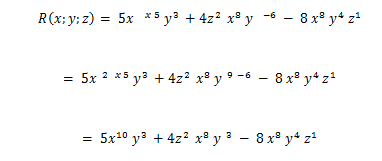



¡Muy buena explicación de los ejercicios del tema! Falta comentar el video.
ResponderEliminar